前記事「音楽のゆらぎの正体」は本コラムの中で最も言いたかった核心部分なのですが、残念ながら私の力不足で誰にでもわかるように説明し切れていないと思います。時々音楽のゆらぎに関して質問のメールをいただくのですが、正しく理解できている方はほとんどいませんでした。感覚的には99パーセントくらいの方が誤解していると感じます。やはり前の記事で述べましたように、音のスペクトルを分析すれば音楽のゆらぎになると誤解している方が圧倒的に多いのです。繰り返しになりますが、それは単なる音の周波数分布であって、ゆらぎでも何でもありません。
もともと音楽のゆらぎというものは非常にわかりにくい概念で正しく伝えることが困難なのですが、少しでも多くの方に理解してもらうために単純な具体例を挙げて説明したいと思います。本記事は10年以上の時間を経て後から追加したものであり、若干順序が前後するところもありますが、より理解を助けるための追加資料としてお読みいただければ幸いです。
楽曲そのもののゆらぎを考える
楽譜は音楽そのものではないが
前記事でも述べましたように、楽譜というものは音楽をどのように演奏するかという指示書であって音楽そのものではありません。同じメロディーであっても演奏する楽器によって印象は異なりますし、歌声も人によってそれぞれ個性があります。人間は機械ではありませんから、音符の長さも数学的にきっちり演奏できるわけはなく、多少のバラツキは必ずあります。また表現として意図的にテンポを揺らすこともありますが、その場合は時間軸が伸び縮みしていると考えられるわけです。
さらに複雑なのはほとんどの音楽において単音で演奏されることは稀で、必ず複数の音が重なり合っていることが普通です。これはいわゆる和音と呼ばれるものですが、同じメロディーであっても和音の付け方によって曲の印象は全く変わります。当然、音楽のゆらぎも違ったものになるでしょう。
したがって、そこまで考えると一つの楽譜から生み出される音楽は無限に存在するということがおわかりでしょう。ですから音楽のゆらぎを評価するのに楽譜そのものを用いるのは無意味であり、本来は実際に演奏された音楽を対象にすべきというのは前記事で述べた通りです。
しかしその方法は少々複雑でわかりにくいため、また誤解を生み出す原因になっていることは今までの経験からはっきりしました。そこで本記事では話を非常に単純化してわかりやすくするために、あえて楽譜そのものを用いて音楽のゆらぎを評価することを考えます。もちろん本来の意味からは正しくないのですが、「純粋に」楽曲そのもののゆらぎを評価するのであればこういうアプローチもあり得るということで理解して下さい。
楽譜を「波形」に変換する
下の楽譜は有名なベートーヴェン「第九」の一節です。「歓喜の歌」として誰もが知っているメロディーですね。

ご存知のように、楽譜というものは横軸に時間、縦軸に音の高さ(音高)を記述していますので、赤線で示したようにそれぞれの音符を線で結んでいけば音高の時間変化を表したグラフになります。音高というのは音の周波数と一対一に対応していますから、言い換えれば周波数の時間変化を表したグラフになります。赤線を眺めれば何となく波形のようなものができ上がるのがおわかりでしょう。ここで横軸を時間(秒)、縦軸を周波数(ヘルツ)に変換するとデジタルデータ化してコンピュータで扱うことが可能になります。
「波形」をフーリエ変換したものは何を表すか?
こうやって得られた「波形」から音楽のゆらぎを評価するには、波形をフーリエ変換してスペクトルに分解してやればよいのです。方法は音のスペクトルを求めるのと全く同じですから、ここでは割愛します。
フーリエ変換といっても理系の人以外には何のことだかわからないと思いますが、簡単に言えば「あらゆる波形は全ての周波数の正弦波の重ね合わせで表すことができる」という数学的な定理に基づいています。正弦波というのは最も単純なサイン波(いわゆる三角関数)のことです。
もっとわかりやすく言いますと、フーリエ変換した結果は元の波形がどの周波数の波をどのくらいの割合で含んでいるかを表しているのです。ここで周波数という言葉を使うとまた誤解の原因になるので、あえて周期と呼ぶことにしましょう。周期というのは周波数の逆数ですからどちらでも同じことです。
では音符を赤線でつないだ波形が何だったかを思い出しますと、これは音高の時間変化を表していたわけです。それをフーリエ変換した結果は、音高がどのくらいの周期で変化しているか、その割合を表すことになります。
音楽には周期性がある
音高が周期的に変化していると言ってもまだピンと来ないでしょうから、もっと具体的に考えてみましょう。上の楽譜をもう一度よく見て下さい。
まず1~2小節目と3~4小節目はそれぞれ上がって下がってというパターンになってますよね。こういうのを楽典では「動機」と呼びます。動機というのは楽曲を構成する最小単位と考えて下さい。あらゆる音楽は細かく見ると動機の積み重ねででき上がっています。
次に5~6小節目は1~2小節目の動機と全く同じものを繰り返します。7~8小節目は3~4小節目の動機と前半部分は全く同じで、後半部分が少し違うだけですね。つまり同じ動機は曲の中で繰り返し現れます。
もう少し大きい単位で見ますと、1~4小節目と5~8小節目はほとんど同じで8小節目だけが違いますね。つまり4小節単位でほとんど同じパターンが繰り返されているわけで、動機を複数個集めてできる一つの単位を小楽節と呼びます。曲全体を眺めてみますと、1~4小節目と5~8小節目、そして13~16小節目はほとんど同じパターンの小楽節が繰り返されており、9~12小節目だけが違うパターンの小楽節であることもわかりますね。
さらに大きい単位で見ますと、1~8小節目で一つの区切りとなっていて、いったん終わった感じになっていますね。そして9小節目からは別の展開が始まり、16小節目で完全に終わります。リピート記号が付いていますから9~16小節目はもう一度繰り返されることになります。このように終止形を伴う小楽節の集まりを大楽節と呼びます。この曲を大きく見れば、1~8小節目、9~16小節目、9~16小節目(繰り返し)という8小節からなる3つの大楽節で構成されていることがわかります。
このように曲を繰り返しのパターンに注目して分解していくと、小さい方から動機・小楽節・大楽節という単位に分割することができます。この曲の場合、それぞれ2小節・4小節・8小節という単位でよく似たパターンが繰り返されていることになります。言い換えますと、動機や楽節というのは音高の時間変化が一定の周期で繰り返されているということですから、その周期が2小節・4小節・8小節に相当するということになるわけです。ここまではおわかりでしょうか?
周期性のタイムスケール
上の例では比較的短い曲について考察しましたが、それでも2~8小節くらいの単位で繰り返しの周期が存在するわけです。これは時間に直すとおよそ数秒~十数秒くらいのスケールになりますね。
クラシックでは曲の形式(楽式)というものが厳格に定義されていて、三部形式・ロンド形式・ソナタ形式、さらにはその複合形式など実に様々な楽式が存在します。それは何もクラシックに限った話ではなく、今日のポピュラー音楽でも全く同じことで、どんな楽曲であろうと独立した細かい部分に分割することができ、それらの組み合わせや繰り返しで曲が成り立っています。たとえば一般的な歌モノで典型的に見られる形式は下図のようなものです。

ここでAメロ・Bメロ、そしてサビといったものがそれぞれ独立した一つのフレーズ(大楽節)として成り立っており、もちろんこれらの大楽節をさらに細かく見れば小楽節や動機に分割することができます。歌モノでは通常Aメロ・Bメロ・サビが2~3コーラス分繰り返されます。そしてその間に間奏が入ったり、前後にイントロやエンディングが付いたりします。やはり同じフレーズが繰り返し登場するわけですから周期性があると言えます。その周期は数十秒から分単位になることもあるでしょう。
一方で周期の短い方に着目すると、動機は通常2小節程度と言いましたが、実際はもっと細かい繰り返しも存在します。たとえば16分音符4個のパターンを数小節にわたって繰り返したり、トリルでさらに細かい音符を連続して往復することもよくあります。その場合の繰り返し周期は数分の1秒程度の短いものになるでしょう。
現実にはほぼあり得ませんが、もし繰り返しの全くない音楽というのが存在したらどうなるでしょう? この場合、最初から最後まで全く同じ部分がないということで、別の見方をすればランダムな音の羅列と考えることもできます。全く規則性のないデータをフーリエ変換すると、低周波成分から高周波成分までほぼ均等に含んだものになります。これはいわゆるホワイトノイズと呼ばれるものです。高周波成分というのは周期が短いということですから、ランダムなデータはきわめて短い周期の変化を豊富に含んでいることになるのです。
このようにして考えると、音楽の周期性には数分の1秒程度の短いものから数分にわたる長いものまで様々なタイムスケールが存在することがわかります。
1/fゆらぎの解釈
1/fゆらぎについてもう一度おさらいしておきましょう。元となる波形データをフーリエ変換すると周波数成分に分解することができて、これを周波数スペクトルと呼びます。要はどの周波数の成分をどのくらいの割合で含んでいるかということがわかるのです。通常は横軸に周波数をとり、縦軸に周波数ごとの強さをとります。オーディオ装置でよく見かけるスペクトラムアナライザーを想像して下さい。あれと全く同じです。音であれば低音から高音までどのくらいの割合で含んでいるかを表しているわけですね。
しかし音楽のゆらぎについて評価する場合、周波数というのは音の周波数のことではありません。ここでほとんどの方が誤解するので絶対に誤解しないようにして下さい。元のデータは何だったかというと、楽譜を音高の時間変化に変換した波形でしたね。それは音の波形とは全く違うのです。音高の時間変化の波形をフーリエ変換して得られる結果は、音高がどのくらいの周期で変化しているか、その割合を表すことになります。ここで周波数という言葉を使うとまた誤解されるので、あえて周期と言いました。周波数は周期の逆数なので同じことなのですが、それは音の周波数とは全く違うことを理解して下さい。なかなか良い表現が見つからないのですが、「音高が変化する速さ」とでも呼べばいいのでしょうか。これが理解できないと先へは進めません。
1/fゆらぎを評価する際には、横軸に周波数(周期の逆数でもあります)の対数、縦軸にスペクトルの強さ(周波数成分が含まれる割合)の対数をとった両対数グラフが用いられます。概念的に示すと下のようなグラフになります。
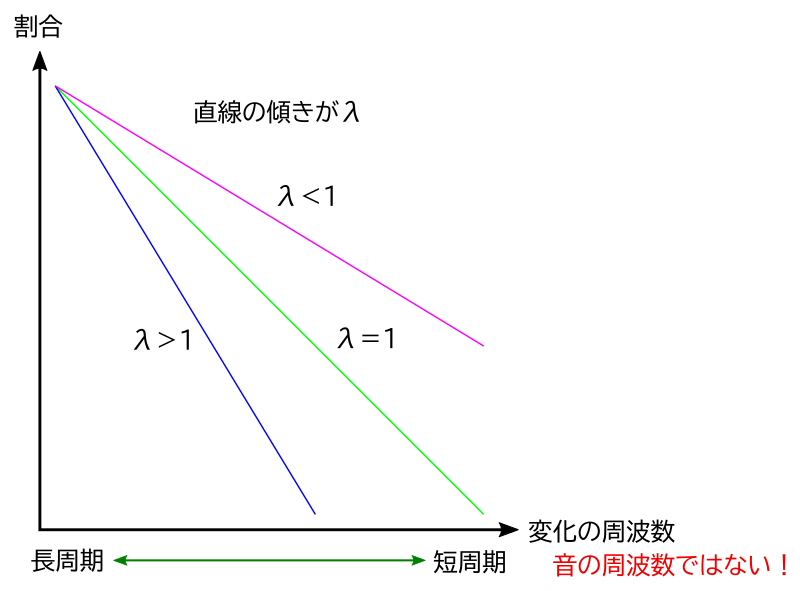
周期は周波数の逆数ですから、横軸は右へ行くほど短周期、左へ行くほど長周期ということになります。周波数に対するスペクトルの強さをプロットしていくともちろん直線にはなりませんが、最小二乗法などを用いるとバラツキを無視して直線で近似することができます。
一般的に周波数が高くなるほどスペクトルは小さくなり、右下がりのグラフになりますが、対数をとっていますので直線で近似した場合は1/fλという形の指数関数を表すことになります。この指数λがゆらぎの程度を表す重要な指標となっており、λが大きいほど直線の傾きは急になります。もしλ=0ならば常に変化しないということですから水平な直線となります。そしてλ=1という特別な場合は1/fとなりますから、これがいわゆる1/fゆらぎに相当します。
ここではλ=1を境として、λが1より大きい場合と1より小さい場合について考えてみましょう。まずλ>1の場合は図の青線で示したように直線の傾きが急になります。このとき周波数が高くなるほど割合は急激に小さくなりますから、短周期の変化はほとんど含まれないということです。音楽的に考えますと必ずしもテンポが遅いという意味ではなく、細かい音符が少なく、しかも規則性が高いということが言えますね。だいたい4分音符より長い音符で構成され、形式がきっちり守られていて似通った部分が多い曲ほどλは大きくなる傾向があります。
逆にλ<1の場合は紫の線で示すように直線の傾きは緩やかになります。この場合は周波数の高い成分をたくさん含んでいるということですから、短周期の変化が多いということになります。音楽的に考えると細かい音符が多い、あるいは似通った部分が少ない(規則性が低い)場合にこのような形になります。その極端な場合がλ=0で、水平な直線になりますから長周期から短周期まで同じ割合で変化していることになり、これは先に述べたようなホワイトノイズになります。たとえばピアノの鍵盤を全くでたらめに弾いたような場合はそれに近い形になるでしょう。
これでλの意味がおおよそおわかりいただけたかと思います。λが大きいほど規則性が高く、変化に乏しい単調な曲調であることを示唆し、λが小さいほど規則性が低く、変化に富んだ曲調であることを示唆します。そしてその中庸がλ=1という1/fゆらぎになるわけです。
1/fゆらぎとは秩序と無秩序のバランスである
上の議論でおわかりいただけたように、λの値は曲の規則性の程度を表す指標と考えられます。つまり繰り返しが多く、形式に則って規則的に作られているほどλは大きくなります。それは「秩序」のある状態だとも言えます。
しかしあまりにも秩序がありすぎると、聴いている方は退屈に感じてしまいます。なぜなら音楽の本質とは、聴き手の予想を裏切ることにあるからです。適度に予想を裏切られることで人は感動を覚えます。もし先の展開が全部予想できてしまえば、あらためて聴く必要もないわけです。極端な話、同じフレーズを延々と繰り返していてもそれは退屈でしかないでしょう。
一方で秩序がなさすぎるのも人は快いとは感じないのです。繰り返しの全くない音楽というのはほとんど存在しませんが、もしあるとすれば前衛音楽のようなものが考えられます。曲の最初から最後までずっと変化しっぱなしで同じ部分が全くない音楽があったとすればどう感じるでしょうか? おそらく人は忙しすぎてついていけないと思います。音楽を聴いて心が休まるどころか逆に疲れてしまうでしょう。
音楽というのは同じフレーズを適度に繰り返すことによって印象を深め、しっかり記憶に残す意図があります。どんなに素敵なフレーズでも一度聴いただけではなかなか覚えられませんからね。しかしあまりにも繰り返しばかりだと今度は退屈に感じてしまい飽きてきます。そこで適度に「予想を裏切る」必要があるのです。聴き手が「次はこう来るだろう」と予想しているところを不意に裏切って全く違う展開に入ったところで人は「あっ!」と感動を覚えるのです。
つまり人にとって心地良い音楽とは、秩序と無秩序のバランス、これが大切なのですね。スペクトル分析の話に戻すと、λ>1は秩序が高い状態、λ<1は秩序が低い状態であり、その中庸であるλ=1こそが秩序と無秩序が適度にバランスした状態と考えられるのです。1/fゆらぎの音楽が人に安らぎを与えると言われる理由はここから来ています。
最後に
最初に述べたように、楽譜そのものから音楽のゆらぎを評価するという手法は本来の意味からすれば不十分です。同じ楽譜であっても演奏者によってそれこそ無限の可能性があるわけですから、演奏者によって新たなゆらぎが生まれます。本来は演奏された音楽を対象にしなければ意味のないことです。
しかしあまりにも1/fゆらぎに関する誤解が多いことから、話をできるだけ単純にするために楽譜そのものから音楽のゆらぎを評価する方法を思いつきました。楽曲そのものが持つゆらぎを純粋に評価したいのであれば、こういうアプローチもあり得るということで理解して下さい。
しつこいほど言いますが(笑)、音の周波数分布をいくら解析しても音楽のゆらぎにはなりません!

コメント
とても参考になる記事ありがとうございます。
インターネットにある情報で参考になるものが少なくて本当に助かりました。
https://www.youtube.com/@nounaionkyo/community
ここの上から7つ目の記事も1/fのゆらぎに関することで共感できる内容でした。参考になればと思い一応載せときます。
ご参考いただきましてありがとうございます。
リンクの記事も読みました。
この方はわかってるなと思いました。
わかりやすく、非常に勉強になりました。
ある作業をする中でベテランと初心者の手の動きを評価すると、ベテランの方が迷いなく手を動かすため規則性が高くなり、初心者は迷いながらするので規則性が低いということを論文で述べたいと思っています。
両対数グラフを書いて、最小二乗法で近似曲線の傾きλを算出し、λが大きいほど規則性が高い、ということを述べた、引用可能な学術論文(可能なら英語)はありますか?
いろいろ検索しましたが、本ページほど明確に書いてある論文が見つからず困っております。
コメントありがとうございます。
確かにベテランと初心者の手の動きもゆらぎの一種として捉えられるかもしれないですね。
残念ながら、学術論文というのは私も知りません。
返信ありがとうございました!
真面目に書いてあるサイトが全く見つからなかったので、助かりました
グラフで示されているように長周期の変化が多くて短周期の変化が少ないっていうのが本来の意図するところっぽいですよね
波が1/fゆらぎって言っているのはそこから来ていそう
オーディオテクニカのサイトに引用で、心臓の鼓動のゆらぎ方が1/fだと発見された、と書いてあるところがありましたが、これは何の周波数と何の関係を見たのかさえわかりませんでした
(低周期の鼓動が一番多いってことなんでしょうか、50BPM~60BPMくらいのデータしかなさそうですが。。)
長周期の変化から短周期の変化まで1/fに比例して含んでいるということです。周期は周波数の逆数ですから、1/fに比例するということは言い換えれば周期に比例するということになります。
低周期の鼓動が一番多いという意味ではありません。人の心拍は安静時であっても常にゆらいでいるので、60BPMと言っても実際には時間的なバラツキがあります。
もし完全に正確であれば心拍スペクトルの成分は60BPMに1本だけしか立ちませんが、少しでもゆらぎがあると低周波から高周波まで多くのスペクトル成分に分解されます。その周波数の傾きが1/fに比例していれば1/fゆらぎということになります。
とても貴重な検証と記事を書き上げてくださりありがとうございます。ピアノ演奏でリズムに縛られない音楽を皆さんに聴いてもらえるよう活動していますが、今回の内容とても勉強になりました!